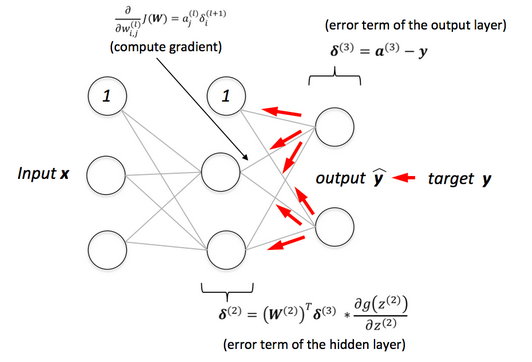
Đạo hàm của tất cả các lớp

Đạo hàm theo các tham số riêng lẻ

Trong bước lan truyền thuận, với giá trị đầu vào x, đầu ra của mạng neural được tính toán. Trong quá trình này, các giá trị kích hoạt $a^l$ tại mỗi lớp được lưu lại để sử dụng sau.

Với mỗi đơn vị j trong lớp đầu ra, tính toán sai số:

$$e^{L}_j = \frac{\partial J}{\partial z^{L}_j}$$

Từ đây, chúng ta có thể suy ra:

$$\frac{\partial J}{\partial w^{L}_{ij}} = a^{L-1}_i e^{L}_j$$ $$\frac{\partial J}{\partial b^{L}_j} = e^{L}_j$$

Với các lớp $l = L-1, L-2, \ldots, 1$, chúng ta tính toán:

$$e^{l}_j = \left( w^{l+1}_j : e^{l+1} \right) f'(z^{l}_j)$$

Cập nhật đạo hàm cho mỗi tham số sẽ là:

$$\frac{\partial J}{\partial w^{l}_{ij}} = a^{l-1}_i e^{l}_j$$ $$\frac{\partial J}{\partial b^{l}_j} = e^{l}_j$$

Đạo hàm theo các ma trận

Việc tính toán đạo hàm cho từng tham số riêng lẻ như đã mô tả ở trên rất dễ để hiểu. Tuy nhiên, trong thực tế, chúng ta cần tối ưu hóa các phép tính bằng cách diễn tả chúng dưới dạng vector và ma trận để tăng tốc độ thuật toán. Ta định nghĩa:

$$e^{l} = \begin{bmatrix} e^{l}_1 \\ e^{l}_2 \\ \vdots \\ e^{l}_{d^{l}} \end{bmatrix} \in \mathbb{R}^{d^{l} \times 1}$$

Bước lan truyền thuận: Với giá trị đầu vào $x$ được cho, tính toán đầu ra của mạng đồng thời lưu lại các giá trị kích hoạt $a^{l}$ tại mỗi lớp.

Với lớp đầu ra, tính toán:

$$e^{L} = \frac{\partial J}{\partial z^{L}}$$

Từ đây, ta suy ra:

$$\frac{\partial J}{\partial W^{L}} = a^{L-1} (e^{L})^T$$ $$\frac{\partial J}{\partial b^{L}} = e^{L}$$

Với các lớp $l = L-1, L-2, \ldots, 1$:

$$e^{l} = \left( W^{l+1} e^{l+1} \right) \odot f'(z^{l})$$

Ở đây, $\odot$ là tích Hadamard (tích từng phần tử), nghĩa là mỗi thành phần của hai vector sẽ được nhân với nhau để tạo ra một vector kết quả.

Cập nhật đạo hàm cho các ma trận trọng số và vector bias

$$\frac{\partial J}{\partial W^{l}} = a^{l-1} (e^{l})^T$$ $$\frac{\partial J}{\partial b^{l}} = e^{l}$$

Lưu ý: Biểu thức đạo hàm ở dòng trước có thể gây ra câu hỏi: tại sao lại là $a^{L-1} (e^{L})^T$ mà không phải là $(a^{L-1})^T e^{L}$ hoặc cách khác? Một quy tắc quan trọng cần nhớ là kích thước của hai ma trận ở phía bên phải phải khớp nhau. Kiểm tra điều này cho thấy rằng vế trái biểu diễn đạo hàm với ma trận $W^{L}$, có kích thước $\mathbb{R}^{d^{L-1} \times d^{L}}$. Do đó, $e^{L} \in \mathbb{R}^{d^{L} \times 1}$ và $a^{L-1} \in \mathbb{R}^{d^{L-1} \times 1}$ có nghĩa là biểu thức đúng phải là $a^{L-1} (e^{L})^T$. Hơn nữa, đạo hàm của một hàm số có giá trị vô hướng với một ma trận sẽ có kích thước tương ứng với ma trận đó.

Lan truyền ngược cho Gradient Descent theo Mini-Batch

Điều gì xảy ra khi chúng ta muốn triển khai Gradient Descent theo mini-batch? Trên thực tế, Mini-batch Gradient Descent là phương pháp được sử dụng phổ biến nhất. Khi tập dữ liệu nhỏ, Gradient Descent theo batch có thể được áp dụng trực tiếp.

Trong trường hợp này, cặp $(X, Y)$ sẽ ở dạng ma trận. Giả sử rằng mỗi lần tính toán xử lý $N$ điểm dữ liệu. Khi đó, ta có:

$$X \in \mathbb{R}^{d^{0} \times N}, \quad Y \in \mathbb{R}^{d^{L} \times N}$$

trong đó $d^{0} = d$ là kích thước của dữ liệu đầu vào (không bao gồm bias).

Do đó, các giá trị kích hoạt sau mỗi lớp sẽ có dạng:

$$A^{l} \in \mathbb{R}^{d^{l} \times N}, \quad E^{l} \in \mathbb{R}^{d^{l} \times N}$$

Ta có thể suy ra các công thức cập nhật như sau.

Bước lan truyền xuôi: Với toàn bộ tập dữ liệu (batch) hoặc một mini-batch của đầu vào $X$, tính toán đầu ra của mạng đồng thời lưu lại các giá trị kích hoạt $A^{l}$ tại mỗi lớp. Mỗi cột của $A^{l}$ tương ứng với một điểm dữ liệu trong $X$.

Với lớp đầu ra, tính toán:

$$E^{L} = \frac{\partial J}{\partial Z^{L}}$$

Từ đây, ta suy ra:

$$\frac{\partial J}{\partial W^{L}} = A^{L-1} (E^{L})^T$$ $$\frac{\partial J}{\partial b^{L}} = \sum_{n=1}^{N} e^{L}_n$$

Với các lớp $l = L-1, L-2, \ldots, 1$:

$$E^{l} = \left( W^{l+1} E^{l+1} \right) \odot f'(Z^{l})$$

Ở đây, $\odot$ chỉ tích từng phần tử, nghĩa là mỗi phần tử của hai ma trận sẽ được nhân để tạo ra ma trận kết quả.

Cập nhật đạo hàm cho các ma trận trọng số và vector bias:

$$\frac{\partial J}{\partial W^{l}} = A^{l-1} (E^{l})^T$$ $$\frac{\partial J}{\partial b^{l}} = \sum_{n=1}^{N} e^{l}_n$$

Phương pháp lan truyền ngược có cấu trúc này, dù là cho Gradient Descent ngẫu nhiên hay theo batch, không chỉ nâng cao sự hiểu biết mà còn tối ưu hóa hiệu quả tính toán trong việc huấn luyện mạng neural.