Nhảy tới nội dung

Mạng nơ-ron nhiều lớp (MLP)

Giới thiệu về Mạng nơ-ron nhân tạo (ANN)​

Mạng nơ-ron nhân tạo (ANN) là một trong những khái niệm cơ bản trong các lĩnh vực trí tuệ nhân tạo (AI) và học máy. Được lấy cảm hứng từ cấu trúc và chức năng của hệ thần kinh trong não người, ANNs là những mô hình tính toán có khả năng học hỏi từ dữ liệu và cải thiện hiệu suất theo thời gian. Chúng đã trở thành nền tảng của nhiều công nghệ hiện đại, bao gồm nhận diện hình ảnh, xử lý ngôn ngữ tự nhiên và xe tự lái, ...

Artificial Neural Networks (ANN)

Nguồn gốc của mạng nơ-ron nhân tạo​

Khái niệm về ANN bắt nguồn từ chức năng của các nơ-ron sinh học trong não người. Mô hình nơ-ron nhân tạo đầu tiên, được gọi là "Perceptron," được phát triển vào năm 1958 bởi nhà khoa học Frank Rosenblatt. Mặc dù Perceptron ban đầu chỉ có thể giải quyết các bài toán tuyến tính, nó đã mở đường cho việc khám phá các mô hình phức tạp hơn, dẫn đến sự phát triển của các mạng nhiều lớp và các thuật toán học sâu hiện đại.

Vấn đề mà ANN giải quyết​

ANN thường được áp dụng cho các bài toán liên quan đến phân loại, dự đoán và nhận diện mẫu. Một vấn đề điển hình mà ANNs giải quyết là phân loại hình ảnh: hệ thống học từ các hình ảnh có nhãn và sau đó dự đoán nhãn của các hình ảnh mới. ANNs cũng được sử dụng trong các nhiệm vụ tối ưu hóa, phân tích hồi quy và dự đoán chuỗi thời gian.

Các lớp trong ANN​

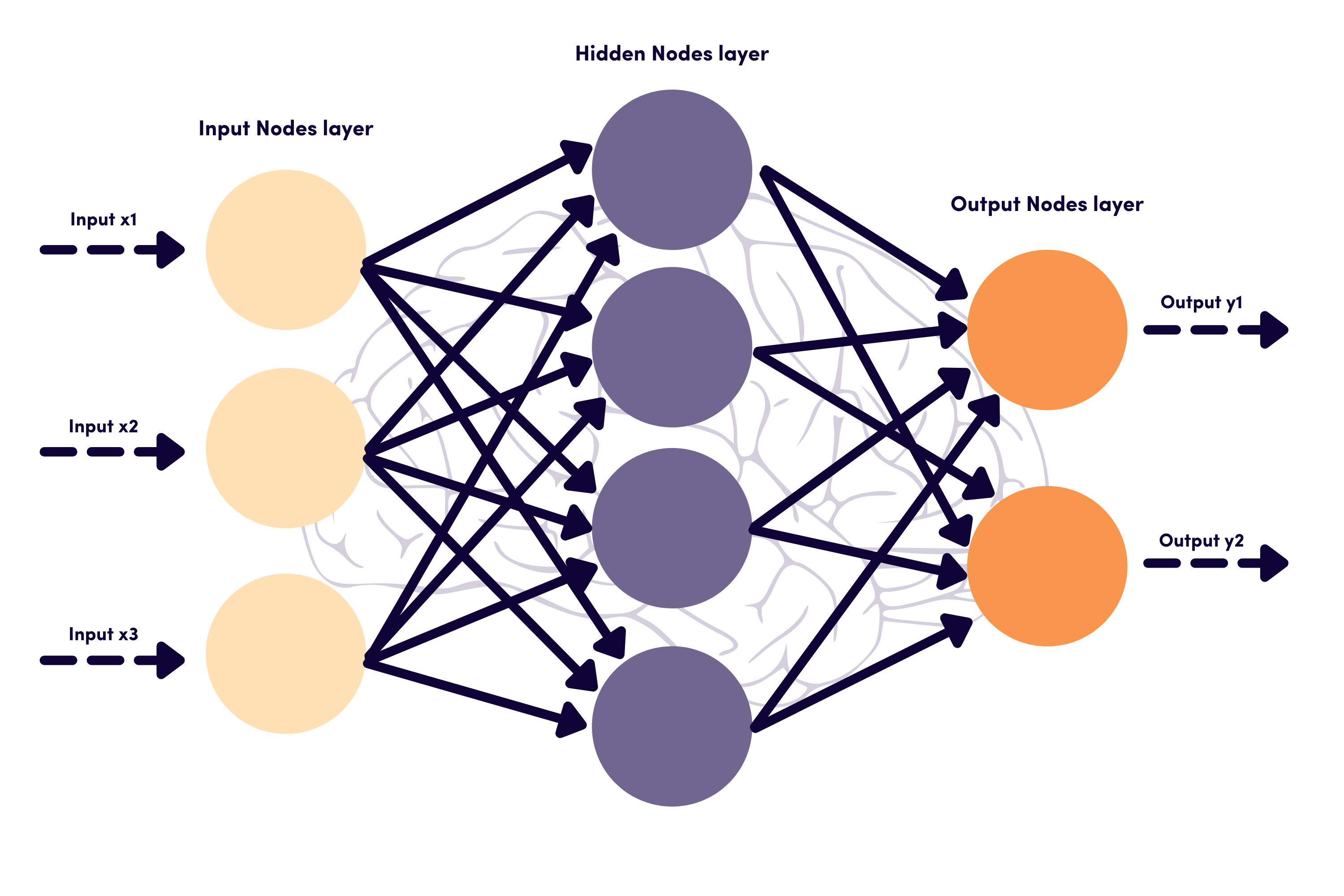
Một Mạng nơ-ron nhân tạo bao gồm nhiều lớp làm việc cùng nhau để xử lý và trích xuất thông tin từ dữ liệu:

  1. Lớp đầu vào: Đây là lớp đầu tiên nhận dữ liệu đầu vào. Mỗi nơ-ron trong lớp này đại diện cho một đặc trưng của dữ liệu.

  2. Lớp ẩn: Nằm giữa lớp đầu vào và lớp đầu ra. Các lớp này trích xuất các đặc trưng từ dữ liệu bằng cách sử dụng các hàm kích hoạt như ReLU (Rectified Linear Unit) hoặc Sigmoid.

  3. Lớp đầu ra: Lớp cuối cùng tạo ra các kết quả dự đoán dựa trên thông tin đã được xử lý trong các lớp ẩn. Số lượng nơ-ron trong lớp này phụ thuộc vào bài toán hiện tại (ví dụ, nếu nhiệm vụ phân loại có ba danh mục, lớp đầu ra sẽ chứa ba nơ-ron).

Các hàm kích hoạt trong ANN​

Các hàm kích hoạt đóng vai trò quan trọng trong việc xác định đầu ra của các nơ-ron trong ANN. Dưới đây là một số hàm kích hoạt phổ biến:

  1. ReLU (Rectified Linear Unit): Hàm ReLU được định nghĩa như sau:

    f(x)=max⁡(0,x)f(x) = \max(0, x)

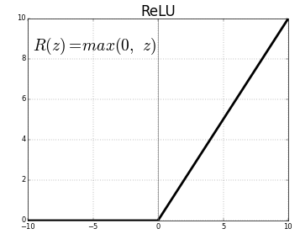
    ReLU Activation Function

    Hàm này được sử dụng rộng rãi trong các lớp ẩn nhờ tính đơn giản và hiệu quả. Ta thấy rằng, khi đạo hàm hàm ReLU, với x < 0 thì f'(x) = 0 và x > 0 thì f'(x) = 1. ReLU cho phép các giá trị dương đi qua trong khi chặn các giá trị âm, dẫn đến việc hội tụ nhanh hơn trong quá trình huấn luyện.

  2. Sigmoid: Hàm Sigmoid được định nghĩa như sau:

    f(x)=11+e−xf(x) = \frac{1}{1 + e^{-x}}

    Sigmoid Activation Function

    Hàm này nén các giá trị đầu vào vào khoảng giữa 0 và 1, làm cho nó phù hợp cho các nhiệm vụ phân loại nhị phân. Tuy nhiên, nó có thể dẫn đến tiêu giảm cho các đầu vào dương hoặc âm lớn, điều này có thể cản trở quá trình học trong các mạng sâu hơn.

  3. Tanh (Hyperbolic Tangent): Hàm Tanh được định nghĩa như sau:

    f(x)=ex−e−xex+e−xf(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}

    Tanh Activation Function

    Nó xuất ra các giá trị nằm giữa -1 và 1, giúp trung tâm hóa dữ liệu quanh zero. Tanh thường hoạt động tốt hơn so với hàm Sigmoid, vì nó giảm thiểu vấn đề gradient biến mất ở mức độ lớn hơn.

  4. Softmax: Hàm Softmax thường được sử dụng trong lớp đầu ra của các bài toán phân loại đa lớp. Nó chuyển đổi các điểm số thô (logits) từ mạng thành xác suất tổng bằng 1, làm cho nó phù hợp với các mô hình cần dự đoán xác suất của mỗi lớp. Công thức của hàm Softmax được cho bởi:

    f(xi)=exi∑jexjf(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}

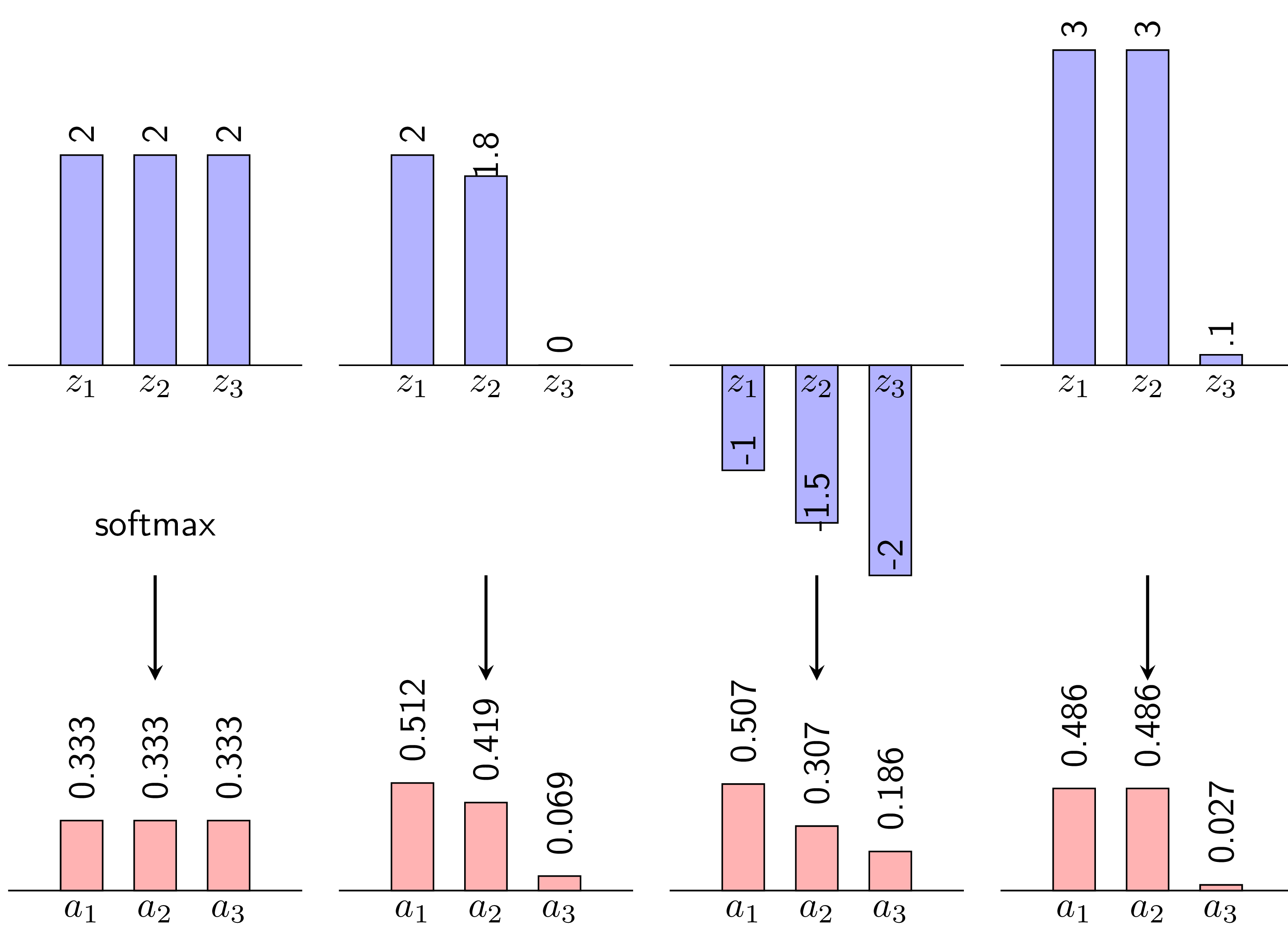
    Softmax Activation Function

    trong đó xix_i là logit cho lớp i và mẫu số tổng hợp trên tất cả các lớp.

Quá Trình Truyền Thông và Lan Truyền Ngược​

Lan truyền thuận (Feed Forward):​

Đây là quá trình đầu tiên trong đó mạng nơ-ron xử lý dữ liệu đầu vào. Dữ liệu chảy từ lớp đầu vào qua các lớp ẩn, và mỗi nơ-ron tính toán đầu ra của nó dựa trên trọng số và hàm kích hoạt. Kết quả cuối cùng là dự đoán được thực hiện bởi lớp đầu ra.

Chúng ta có thể biểu diễn quá trình truyền tiến một cách toán học như sau:

a0=xa^{0} = x zl=Wlal−1+bl,l=1,2,…,Lz^l = W^l a^{l-1} + b^l, \quad l = 1, 2, \ldots, L al=f(zl),l=1,2,…,La^l = f(z^l), \quad l = 1, 2, \ldots, L y^=al\hat{y} = a^l

Giả sử f:[a,b]→Rf:[a,b] \to \R là khả tích Riemann. Giả sử F:[a,b]→RF:[a,b]\to\R là F(x)=∫axf(t)dtF(x)= \int_{a}^{x}f(t)dt. Thì FF là liên tục, và tại mọi xx mà ff liên tục tại xx, FF khả vi tại xx với F′(x)=f(x)F'(x)=f(x).

Trong đó:

  • ala^l là độ kích hoạt của lớp l
  • zlz^l là tổng trọng số của các đầu vào đến lớp l
  • WlW^l và blb^l là trọng số và độ chệch của lớp l
  • ff là hàm kích hoạt
  • y^\hat{y} là đầu ra dự đoán
  • xx là dữ liệu đầu vào
  • LL là tổng số lớp trong mạng
  • ll là chỉ số lớp

Feed Forward Process

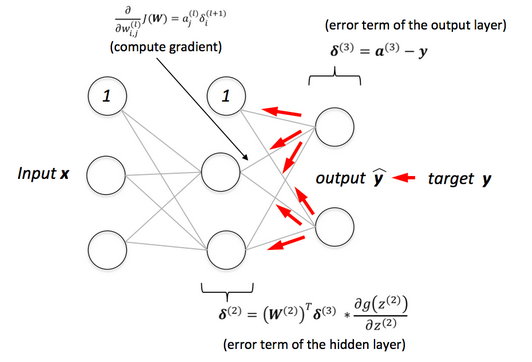
Lan Truyền Ngược:​

Sau khi có được dự đoán, mô hình so sánh nó với giá trị thực và tính toán sai số bằng cách sử dụng hàm mất mát. Quá trình lan truyền ngược liên quan đến việc gửi sai số quay ngược qua mạng, từ các lớp đầu ra đến các lớp đầu vào. Trọng số của các nơ-ron được cập nhật dựa trên các đạo hàm của hàm mất mát, giúp giảm sai số trong các vòng huấn luyện tiếp theo.

Backpropagation Process

Giảm Gradient Ngẫu Nhiên (SGD)​

Giảm Gradient Ngẫu Nhiên (SGD) là một kỹ thuật tối ưu hóa được sử dụng để tính toán các đạo hàm cho ma trận trọng số và độ chệch dựa trên một cặp dữ liệu huấn luyện (x,y)(x, y). Để đơn giản hóa, giả sử JJ đại diện cho một hàm mất mát liên quan đến cặp này, trong đó JJ có thể là bất kỳ hàm mất mát nào, không giới hạn ở MSE (Mean Squared Error).

Đạo hàm của hàm mất mát đối với một trọng số cụ thể trong lớp cuối cùng có thể được biểu diễn như sau:

∂J∂wijl=∂J∂zjl⋅∂zjl∂wijl=ejl⋅aiL−1\frac{\partial J}{\partial w^l_{ij}} = \frac{\partial J}{\partial z^l_j} \cdot \frac{\partial z^l_j}{\partial w^l_{ij}} = e^l_j \cdot a^{L-1}_{i}

Ở đây, ejl=∂J∂zjle^l_j = \frac{\partial J}{\partial z^l_j} thường dễ dàng tính toán, và ∂zjl∂wijl=aiL−1\frac{\partial z^l_j}{\partial w^l_{ij}} = a^{L-1}_{i}, vì zjl=(wjl)TaL−1+bjlz^l_j = (w^l_j)^{T} a^{L-1} + b^l_j.

Tương tự, đạo hàm của hàm mất mát với trọng số độ chệch trong lớp cuối cùng được cho bởi:

∂J∂bjl=∂J∂zjl⋅∂zjl∂bjl=ejl\frac{\partial J}{\partial b^l_j} = \frac{\partial J}{\partial z^l_j} \cdot \frac{\partial z^l_j}{\partial b^l_j} = e^l_j

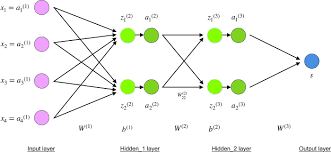
Để xác định các đạo hàm cho các trọng số trong các lớp trước đó, hãy xem cấu trúc như trong sơ đồ dưới đây. Ở đây, đầu vào z và đầu ra a của mỗi đơn vị được ghi rõ để dễ hiểu. Đạo hàm có thể được tính toán như sau:

∂J∂wijl=∂J∂zjl⋅∂zjl∂wijl=ejl⋅ail−1\frac{\partial J}{\partial w^l_{ij}} = \frac{\partial J}{\partial z^l_j} \cdot \frac{\partial z^l_j}{\partial w^l_{ij}} = e^l_j \cdot a^{l-1}_{i}

với

ejl=∂J∂zjl=∂J∂ajl⋅∂ajl∂zjl=(∑k=1dl+1∂J∂zkl+1⋅∂zkl+1∂ajl)f′(zjl)e^l_j = \frac{\partial J}{\partial z^l_j} = \frac{\partial J}{\partial a^l_j} \cdot \frac{\partial a^l_j}{\partial z^l_j} = \left( \sum_{k=1}^{d^{l+1}} \frac{\partial J}{\partial z^{l+1}_{k}} \cdot \frac{\partial z^{l+1}_{k}}{\partial a^l_j} \right) f' (z^l_j)

Phép tổng trong phương trình thứ hai xuất hiện vì (a^l_j) ảnh hưởng đến việc tính toán tất cả các zkl+1z^{l+1}_{k}, với k=1,2,…,dl+1k = 1, 2, \ldots, d^{l+1}. Đạo hàm bên ngoài dấu ngoặc nhấn mạnh rằng ajl=f(zjl)a^l_j = f(z^l_j).

Từ quá trình này, rõ ràng là việc tính toán ejle^l_j là rất quan trọng. Hơn nữa, để xác định các giá trị này, cần tính toán ejl+1e^{l+1}_j từ lớp đầu ra quay ngược đến lớp đầu vào. Quá trình tính toán quay ngược này tạo ra thuật ngữ "lan truyền ngược."

Tóm lại, việc tính toán đạo hàm trong SGD có thể được tóm tắt như sau:

  1. Tính toán các đạo hàm bằng cách sử dụng lan truyền ngược.
  2. Cập nhật các tham số mô hình dựa trên các đạo hàm đã tính toán và tỷ lệ học.

Cách tiếp cận này đảm bảo huấn luyện hiệu quả các mô hình trong khi xử lý các cập nhật ngẫu nhiên một cách hiệu quả.

Tiếp theo, chúng ta sẽ đi sâu vào khái niệm lan truyền ngược (backpropagation) một cách chi tiết hơn, khám phá cách mà các lỗi được lan truyền qua mạng và cách các trọng số được cập nhật để giảm thiểu các lỗi này.