Bài toán Định Thời Trong HPC

Định thời là một bài toán quan trọng trong các hệ thống tính toán hiệu năng cao (HPC), nơi nhiều tác vụ hoặc công việc cần được phân bổ đến các tài nguyên có sẵn một cách hiệu quả và tối ưu. Mục tiêu của định thời là tối đa hóa việc sử dụng hệ thống, giảm thiểu thời gian hoàn thành công việc và đảm bảo phân bổ tài nguyên công bằng cho các người dùng hoặc ứng dụng khác nhau. Nói một cách đơn giản, bài toán này liên quan đến việc phát triển ba thành phần chính, như hình dưới đây:

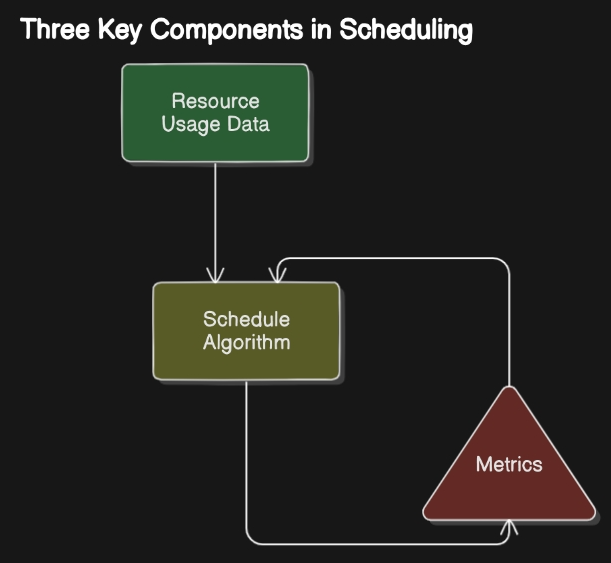
Bối Cảnh

Sơ đồ dưới đây về vòng đời công việc trong hệ thống HPC cho thấy các giai đoạn khác nhau của một công việc từ khi gửi đến khi hoàn thành:

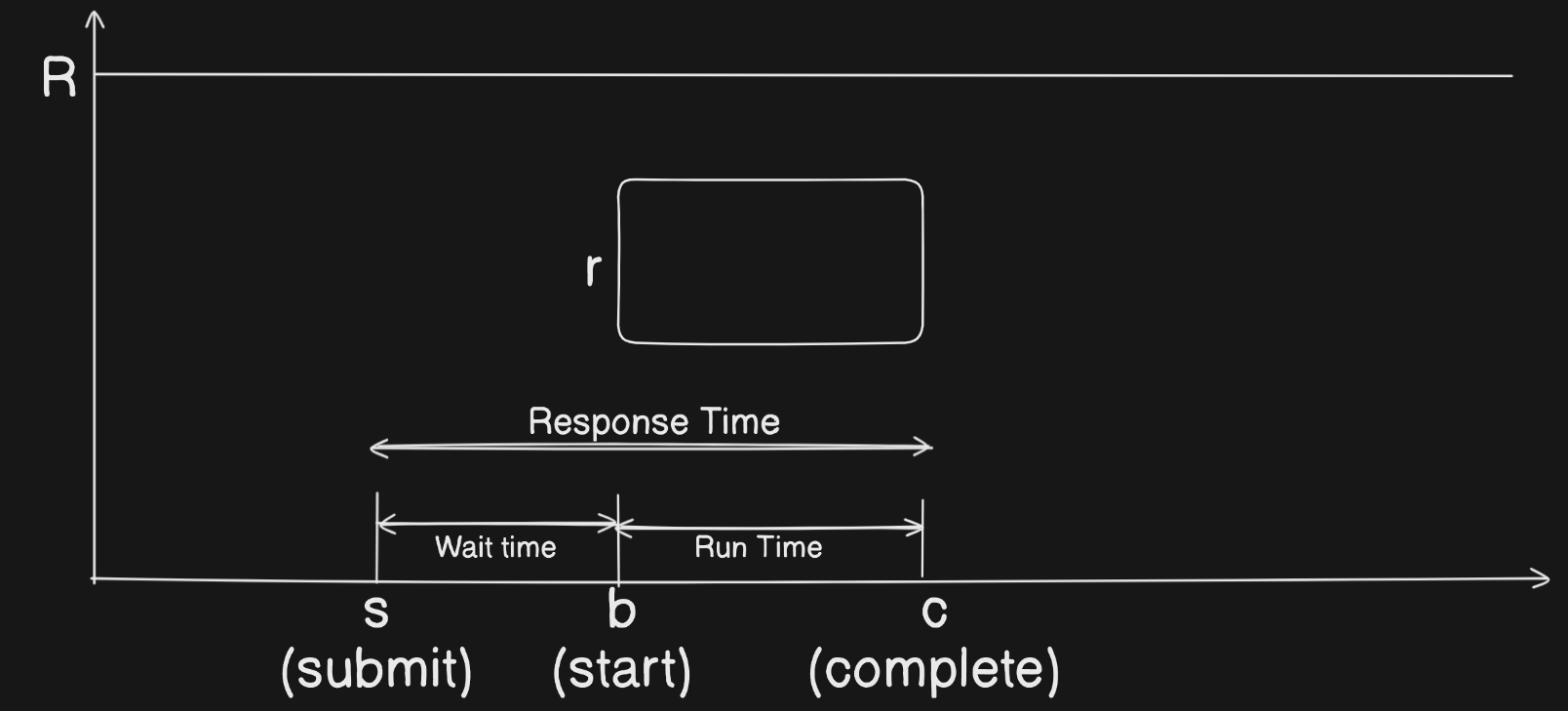
Thông thường, các công việc đến hệ thống tại thời điểm gửi của chúng $s_i$. Sau đó, chúng sẽ được xếp hàng trong hệ thống cho đến khi được lập lịch để chạy trên các tài nguyên có sẵn. Khi một công việc được lập lịch, nó bắt đầu thực thi trên các tài nguyên đã được phân bổ vào thời điểm bắt đầu $b_i$. Thời gian nó phải chờ trong hàng là thời gian chờ $Q_i$:

$$Q_i = b_i - s_i$$

Sau khi công việc bắt đầu, nó thực hiện trong khoảng thời gian chạy của nó $D_i$ và hoàn thành tại thời điểm hoàn thành $c_i$:

$$D_i = c_i - b_i.$$

Tổng thời gian mà một công việc ở trong hệ thống được gọi là thời gian phản hồi $F_i$:

$$F_i = c_i - s_i = Q_i + D_i.$$

Công việc sử dụng tài nguyên trong thời gian chạy của nó như được mô tả trong phương trình sau:

$$r_j(t) = \begin{cases} r_j, & \text{nếu } b_j \leq t < c_j \\ 0, & \text{khác} \end{cases}$$

và giả sử tổng số tài nguyên trong cụm là 𝑅, ràng buộc sau đây áp dụng:

$$\forall t : \sum_{j \in J} r_j(t) \leq R$$

Trong đó:

t đại diện cho một thời điểm.

J là tập hợp các công việc trong lịch.

Các Chỉ Số Để Lập Lịch

Thời Gian Phản Hồi Trung Bình

Thời gian phản hồi trung bình $AF(J)$ được cho bởi:

$$AF(J) = \frac{1}{|J|} \sum_{j \in J} F_j$$

trong đó J đại diện cho tập hợp các công việc trong lịch.

Chỉ số này đo lường thời gian trung bình mà một công việc dành trong hệ thống từ khi gửi đến khi hoàn thành. Thời gian phản hồi trung bình thấp hơn cho thấy hiệu suất tốt hơn về thời gian hoàn thành công việc.

Tăng Trưởng Giới Hạn Trung Bình

Tăng trưởng giới hạn trung bình $BSLD(J)$ được cho bởi:

$$BSLD(J) = \frac{1}{|J|} \sum_{j \in J} \max \left( 1, \frac{F_j}{\max(D_j, k)} \right)$$

trong đó $k$ là một giới hạn dưới

Đây là một chỉ số phổ biến trong lập lịch công việc HPC, được tính toán như tỷ lệ giữa thời gian phản hồi và thời gian chạy. Bởi vì các công việc rất ngắn có thể ảnh hưởng không cân xứng đến Tăng Trưởng Trung Bình.

Mặc dù việc thêm $k$ giúp hạn chế ảnh hưởng của các công việc ngắn, nhưng nó cũng có thể có tác động tiêu cực. Đối với các công việc mà $D_j < k < F_j$, BSLD trở lại thành Thời Gian Lưu Thông Trung Bình (AF), và các công việc có thời gian phản hồi dưới $k$ sẽ không còn đóng góp vào chỉ số này.

Thời Gian Phản Hồi Trung Bình Có Trọng Số Diện Tích (AWF)

Trong lập lịch công việc HPC, Thời Gian Phản Hồi Có Trọng Số Diện Tích (AWF) là một chỉ số quan trọng được sử dụng để đánh giá hiệu quả đóng gói. AWF tối thiểu hóa tổng trọng số thời gian hoàn thành công việc, với trọng số công việc đại diện cho "nỗ lực" cần thiết, thường được gọi là "diện tích" (sử dụng tài nguyên × thời gian chạy).

AWF có một số lợi ích:

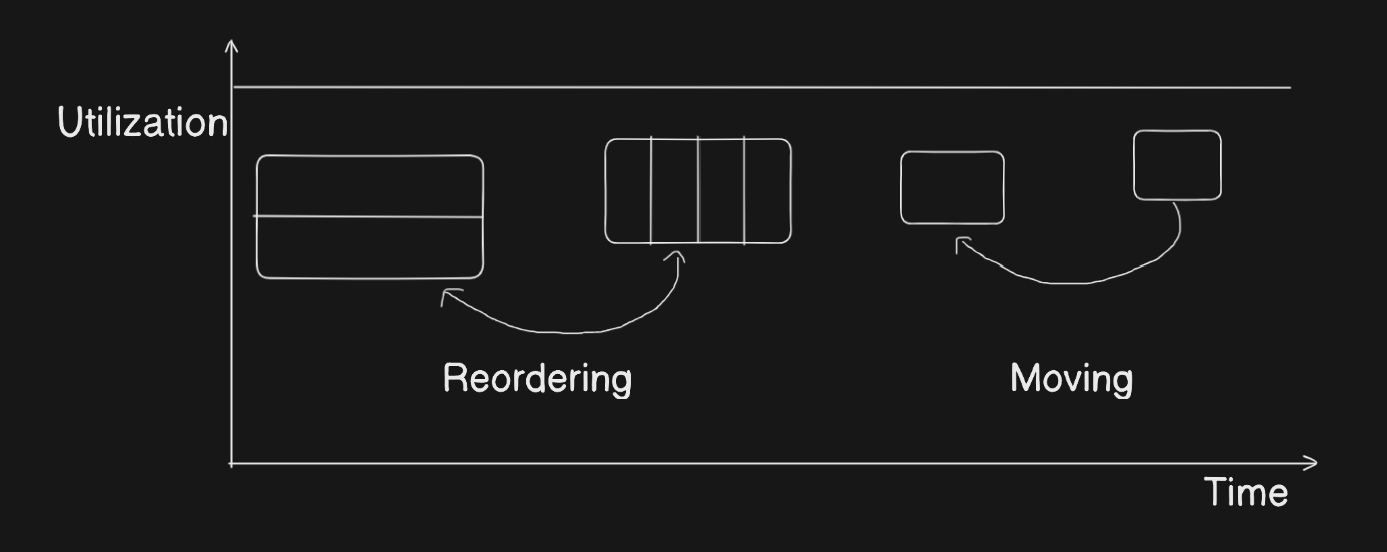
1. Bắt đầu một công việc sớm hơn trong khi giữ nguyên các thời điểm bắt đầu khác sẽ giảm AWF.
2. Sắp xếp lại các công việc mà không thay đổi hồ sơ sử dụng tài nguyên sẽ không ảnh hưởng đến AWF.
3. Chia nhỏ hoặc kết hợp các công việc (trong khi giữ nguyên việc sử dụng tài nguyên) sẽ không ảnh hưởng đến AWF.

Thời Gian Phản Hồi Có Trọng Số Diện Tích (AWF) được cho bởi:

$$AWF(J) = \frac{\sum_{j \in J} r_j D_j F_j}{\sum_{j \in J} r_j D_j}$$

Thời Gian Phản Hồi Cụ Thể Có Trọng Số Ưu Tiên Cấp-α (PαSF)

Khi đề cập đến ưu tiên công việc, chúng ta có thể hiểu hai khái niệm khác nhau:

1. Ưu tiên dựa trên tính hữu ích của công việc: Loại ưu tiên này phản ánh hiệu quả mã của một công việc hoặc tầm quan trọng của dự án liên quan. Trong trường hợp này, các trọng số trong Thời Gian Phản Hồi Có Trọng Số Diện Tích (AWF) có thể được điều chỉnh thành $w_j = p_j r_j D_j$, trong đó $p_j$ đại diện cho ưu tiên của công việc $j$. Sự điều chỉnh này là đơn giản và không cần thêm giải thích.

2. Ưu tiên dựa trên sự công bằng: Ở đây, trọng tâm chuyển sang ý tưởng rằng các công việc đã chờ đợi lâu hơn nên được ưu tiên. Để duy trì tính độc lập của chỉ số mới này với kích thước công việc, chúng tôi đề xuất một phương pháp trong đó các công việc được cấu thành từ các "đơn vị tính toán" vô hạn, mỗi đơn vị cần $dr$ tài nguyên và $dt$ thời gian chạy. Chỉ số Thời Gian Phản Hồi Cụ Thể Có Trọng Số Ưu Tiên Cấp-α (PαSF), được định nghĩa là:

$$PαSF(J) = \frac{\alpha + 1}{\alpha + 2} \cdot \frac{\sum r_j (F_j^{\alpha + 2} - Q_j^{\alpha + 2})}{\sum r_j (F_j^{\alpha + 1} - Q_j^{\alpha + 1})},$$

cân bằng giữa sự công bằng và hiệu quả đóng gói. Tham số $\alpha$ điều chỉnh sự cân bằng này, với các giá trị lớn hơn của $\alpha$ sẽ tạo ra nhiều trọng số hơn cho sự công bằng. Một khoảng hợp lý cho $\alpha$ là từ 1 đến 3, vì các giá trị lớn hơn 3 có thể nhấn mạnh không cân xứng đến các công việc bị lập lịch kém và giảm tính nhạy cảm tổng thể của chỉ số.

PαSF, cùng với AWF, cung cấp một quan điểm tinh tế để đánh giá các thuật toán lập lịch, tiết lộ những lợi thế và nhược điểm mà các chỉ số truyền thống như BSLD thường bỏ qua.

Mất Công Suất (LoC)

Một chỉ số khác được đề xuất để đo lường việc đóng gói công việc là Mất Công Suất (LOC)

$$LOC = \frac{ \int_{\min\limits_{1 \leq j \leq n} (s_j)}^{\max\limits_{1 \leq j \leq n} (c_j)} \min (\sum\limits_{j : s_j < t < b_j} r_j, R - \sum\limits_{j : b_j < t < c_j} r_j) dt }{ (\max\limits_{1 \leq j \leq n} (c_j) - \min\limits_{1 \leq j \leq n} (s_j)) \times R }$$

Trong đó:
- $ R $ là tổng số nút trong cụm.
- $ c_j $ là thời gian hoàn thành của công việc $ j $.
- $ s_j $ là thời gian bắt đầu của công việc $ j $

Mô phỏng bài toán định thời bằng pybatsim